Question

How would the period of a simple pendulum be affected if it were located on the moon instead of the earth?

Answer 1

On moon time period will become 2.45 times of the time period on earth

Step-by-step explanation:

Time period of simple pendulum is equal to
`T=2\pi \sqrt{(l)/(g)}` ....eqn 1 here l is length of the pendulum and g is acceleration due to gravity on earth

As when we go to moon, acceleration due to gravity on moon is
`(1)/(6)` times os acceleration due to gravity on earth

So time period of pendulum on moon is equal to

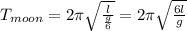`T_(moon)=2\pi \sqrt{(l)/((g)/(6))}=2\pi \sqrt{(6l)/(g)}` --------eqn 2

Dividing eqn 2 by eqn 1

`(T_(moon))/(T)=\sqrt{(6l)/(g)* (g)/(l)}`

`T_(moon)=√(6)T=2.45T`

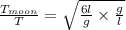
So on moon time period will become 2.45 times of the time period on earth