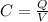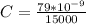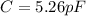To solve this problem we will apply the concepts of the potential difference such as the product between the electric field and the distance, then we will use two definitions of capacitance, the first depending on the Area and the second depending on the load to find the Area. Finally we will look for capacitance with the values already obtained in the first sections of this problem
PART A) Potential Difference is

Here,
E = Electric Field
d = Distance
Replacing,
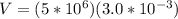
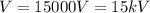
PART B) Capacitance of the capacitor is
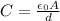
Here,
A = Area
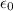 = Permittivity Vacuum
= Permittivity Vacuum
d = Distance
Rearranging to find the Area we have,
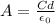
We know at the same time that Capacitance is the charge per Voltage, then
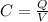
Replacing at this equation we have that
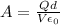
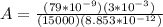
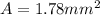
PART C)
Capacitance is given by,