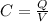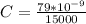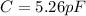Question

The plates of a parallel-plate capacitor are 3.00 mm apart, and each carries a charge of magnitude 79.0 nC. The plates are in vacuum. The electric field between the plates has a magnitude of 5.00 x 10^6 V/m.

Part A) What is the potential difference between the plates?Part B) What is the area of each plate?Part C) What is the capacitance?

Answer 1

To solve this problem we will apply the concepts of the potential difference such as the product between the electric field and the distance, then we will use two definitions of capacitance, the first depending on the Area and the second depending on the load to find the Area. Finally we will look for capacitance with the values already obtained in the first sections of this problem

PART A) Potential Difference is

`V = Ed`

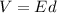
Here,

E = Electric Field

d = Distance

Replacing,

`V = (5*10^6)(3.0*10^(-3))`

`V = 15000V= 15kV`

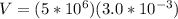
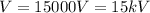
PART B) Capacitance of the capacitor is

`C = (\epsilon_0 A)/(d)`

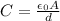
Here,

A = Area

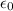`\epsilon_0` = Permittivity Vacuum

d = Distance

Rearranging to find the Area we have,

`A = (Cd)/(\epsilon_0)`

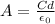
We know at the same time that Capacitance is the charge per Voltage, then

`C = (Q)/(V)`

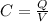
Replacing at this equation we have that

`A = (Qd)/(V\epsilon_0)`

`A = ((79*10^(-9))(3*10^(-3)))/((15000)(8.853*10^(-12)))`

`A = 1.78mm^2`

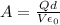
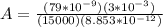
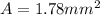
PART C)

Capacitance is given by,

`C = (Q)/(V)`

`C =(79*10^(-9))/(15000)`

`C =5.26pF`