Question

3 lines are shown. A line with points M, H, K intersects with a line with points J, H, L at point H. Another line extends from point H to point N in between angle K, H, J. Angle M H L is (3 x + 20) degrees, angle K H N is (x + 25) degrees, and angle J H N is (x + 20) degrees. What is the measure of AngleJHN? 25° 45° 50° 95°

Answer 1

it's B

Explanation:

Answer 2

Option B.

Explanation:

Given information: ∠MHL=(3x+20), ∠KHN=(x+25), and ∠JHN=(x+20).

We need to find the measure of ∠JHN.

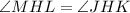`\angle MHL=\angle JHK` (Vertical opposite angles)

`\angle MHL=\angle JHN+\angle KHN`

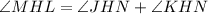
Substitute the given values.

`3x+20=(x+20)+(x+25)`

`3x+20=2x+45`

`3x-2x=45-20`

`x=25`

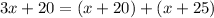
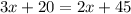
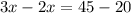
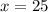
The value of x is 25. So, the measure of ∠JHN is

`\angle JHN=x+20=25+20=45`

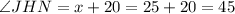
The measure of ∠JHN is 45°.

Therefore, the correct option is B.