Answer:
Option B.
Explanation:
Given information: ∠MHL=(3x+20), ∠KHN=(x+25), and ∠JHN=(x+20).
We need to find the measure of ∠JHN.
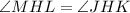 (Vertical opposite angles)
(Vertical opposite angles)
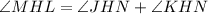
Substitute the given values.
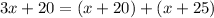
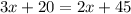
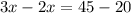
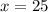
The value of x is 25. So, the measure of ∠JHN is
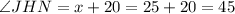
The measure of ∠JHN is 45°.
Therefore, the correct option is B.