Question

A horizontal curve on a two-lane highway (10-ft lanes) is designed for 50 mi/h with a 6% superelevation. The central angle of the curve is 35 degrees and the PI is at station 482 + 72. What is the station of the PTand how many feet have to be cleared from the lane's shoulder edge to provide adequate stopping sight distance?

Answer 1

The PT station is at 485+20.02 and 21.92 ft are to be cleared from the lane's shoulder to provide adequate stopping sight distance.

Step-by-step explanation:

From table 3.5 of Traffic Engineering by Mannering

R_v=835

R=835+(10ft/2)= 840 ft.

Now T is given as

T=R tan(Δ/2)

Here Δ is the central angle of curve given as 35°

So

T=R tan(Δ/2)

T=840 x tan(35/2)

T=840 x tan(17.5)

T=264.85

Now

STA PC=482+72-(2+64.85)=480+07.15

Also L is given as

L=(π/180)RΔ

Here R is the radius calculated as 840 ft, Δ is the angle given as 35°.

L=(π/180)RΔ

L=(π/180)x840 x35

L=512.87 ft

STA PT=480+07.15+5+12.87=485+20.02

Now Ms is the minimum distance which is given as

`M_s=R_v(1-cos((90 * SSD)/(\pi Rv)))\\`

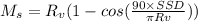
Here R_v is given as 835

SSD for 50 mi/hr is given as 425 ft from table 3.1 of Traffic Engineering by Mannering

So Ms is

`M_s=R_v(1-cos((90 * SSD)/(\pi Rv)))\\M_s=835(1-cos((90 * 425)/(\pi 835)))\\M_s=26.92 ft`

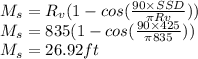
Now for the clearance from the inside lane

Ms=Ms-lane length

Ms=26.92-5= 21.92 ft.

So the PT station is at 485+20.02 and 21.92 ft are to be cleared from the lane's shoulder to provide adequate stopping sight distance.