Question

The volume of air in one beach ball is 288π in 3. What is the volume of air in a ball whose radius is 3 inches greater than the first beach ball?

Answer 1

v_2 = 972 π inch^3

Step-by-step explanation:

Given data:

volume of air V_1 = 288π inc^3

radius of ball at 1 beach = r_1

radius of ball at 2nd beach = r_1 + 3

we know that
`V_1 = 288 \pi`

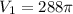
we know that volume is given as
`v_1 =  (4)/(3) \pi r_1^3`

so equating both side of volume we get

`288\pi =  (4)/(3) \pi r_1^3`

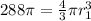
r_1 = 6 inch

therefore r_2 = 9 inch

volume of air at 2nd beach
`v_2 =  (4)/(3) \pi 9^3`

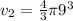
v_2 = 972 π inch^3