Answer:
a) For this case we can see on the y axis the test scores and on the x axis the hours of homework. And as we can see we have a proportional relationship, because when the hours of homework increase the test scores increases too. If we fit a lineal model between y and x we will see an slope positive and a correlation coefficient positive based on the data observed.
b)
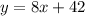
And we want to predict the test score for x = 3hr of homework we just need to replace the value of x=3 in the linear model and we got:
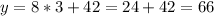
And that would be our predicted value for 3 h of homework
Explanation:
For this case we consider the scatter plot attached to solve the problem.
Part a
For this case we can see on the y axis the test scores and on the x axis the hours of homework. And as we can see we have a proportional relationship, because when the hours of homework increase the test scores increases too. If we fit a lineal model between y and x we will see an slope positive and a correlation coefficient positive based on the data observed.
Part b
Assuming the following linear model for the situation:
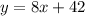
And we want to predict the test score for x = 3hr of homework we just need to replace the value of x=3 in the linear model and we got:
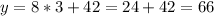
And that would be our predicted value for 3 h of homework