Answer: The standard deviation is 0.0998. The 10% condition is met because it is very likely there are more than 250 fish in the river.
Explanation:
The standard deviation of the sampling distribution =
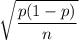 , where p= population proportion and n = sample size.
, where p= population proportion and n = sample size.
Let p be the proportion of fish in a river are catfish.
As per given , we have
p= 0.47
n= 25
The, the standard deviation of the sampling distribution will be
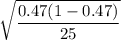
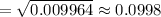
The 10% condition : Sample sizes should be no more than 10% of the population.
But a river can have more than 250 fish [where 10% of 250 =25 (sample size)]
i.e. The 10% condition is met because it is very likely there are more than 250 fish in the river.
So the correct answer is "The standard deviation is 0.0998. The 10% condition is met because it is very likely there are more than 250 fish in the river."