Question

Forty-seven percent of fish in a river are catfish. Imagine scooping out a simple random sample of 25 fish from the river and observing the sample proportion of catfish. What is the standard deviation of the sampling distribution? Determine whether the 10% condition is met.

The standard deviation is 0.0998. The 10% condition is not met because there are less than 250 fish in the river.

The standard deviation is 0.0998. The 10% condition is met because it is very likely there are more than 250 fish in the river.

The standard deviation is 0.9002. The 10% condition is met because it is very likely there are more than 250 fish in the river.

The standard deviation is 0.9002. The 10% condition is not met because there are less than 250 fish in the river.

We are unable to determine the standard deviation because we do not know the sample mean. The 10% condition is met because it is very likely there are more than 250 fish in the river.

Answer 1

The standard deviation is 0.0998. The 10% condition is met because it is very likely there are more than 250 catfish in the river.

Explanation:

I got it right on the quiz

Answer 2

Answer: The standard deviation is 0.0998. The 10% condition is met because it is very likely there are more than 250 fish in the river.

Explanation:

The standard deviation of the sampling distribution =
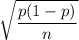`\sqrt{(p(1-p))/(n)}` , where p= population proportion and n = sample size.

Let p be the proportion of fish in a river are catfish.

As per given , we have

p= 0.47

n= 25

The, the standard deviation of the sampling distribution will be
`\sqrt{(0.47(1-0.47))/(25)}`

`=√(0.009964)\approx0.0998`

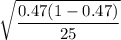
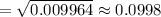
The 10% condition : Sample sizes should be no more than 10% of the population.

But a river can have more than 250 fish [where 10% of 250 =25 (sample size)]

i.e. The 10% condition is met because it is very likely there are more than 250 fish in the river.

So the correct answer is "The standard deviation is 0.0998. The 10% condition is met because it is very likely there are more than 250 fish in the river."