Answer:
x=±0.026m
Step-by-step explanation:
In simple harmonic motion the maximum value of the magnitude of velocity
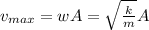
The speed as a function of position for simple harmonic oscillator is given by

where A is amplitude of motion
Given data
Amplitude A=3 cm =0.03 m
v=(1/2)Vmax
To find
We have asked to find position x does its speed equal half of is maximum speed
Solution
The speed of the particle the maximum speed as:
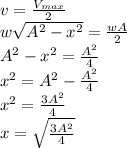
x=±(√3(0.03)/2)
x=±0.026m