Question

A particle executes simple harmonic motion with an amplitude of 3.00 cm. At what position does its speed equal half of is maximum speed?

Answer 1

The speed of a particle in simple harmonic motion is half of its maximum speed when it is at a position that is 1/2 of its amplitude.

Step-by-step explanation:

In simple harmonic motion, the speed of a particle is maximum at the equilibrium position and decreases as it moves away from the equilibrium. The speed is equal to half of its maximum speed when the particle is at a position that is 1/2 of its amplitude. Since the amplitude is given as 3.00 cm, the position where the speed is half of its maximum speed would be at 1.50 cm.

Answer 2

x=±0.026m

Step-by-step explanation:

In simple harmonic motion the maximum value of the magnitude of velocity

`v_(max)=wA=\sqrt{(k)/(m) }A`

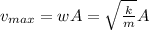
The speed as a function of position for simple harmonic oscillator is given by

`v=w\sqrt{A^(2)-x^(2)`

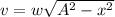
where A is amplitude of motion

Given data

Amplitude A=3 cm =0.03 m

v=(1/2)Vmax

To find

We have asked to find position x does its speed equal half of is maximum speed

Solution

The speed of the particle the maximum speed as:

`v=(V_(max) )/(2)\\ w\sqrt{A^(2)-x^(2) }=(wA)/(2)\\ A^(2)-x^(2)=(A^(2) )/(4)\\ x^(2)=A^(2)- (A^(2) )/(4)\\ x^(2)=(3A^(2))/(4) \\x=\sqrt{(3A^(2))/(4)}`

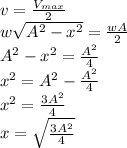
x=±(√3(0.03)/2)

x=±0.026m