The inequality that represent age of marcus is:
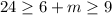
The possible values for age of Marcus is:
m = 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18
Solution:
Given that,
The sum of ages of Kevin and Marcus was at least 9 years but was at most 24 years
Kevin is 6 years old
Let "m" be the age of Marcus
Thus we frame a inequality as:
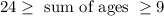
at least 9 years means that "greater than or equal to 9"
at most 24 years means "less than or equal to" 24
From given,
Sum of ages = kevin age + marcus age
Sum of ages = 6 + m
Thus the inequality is:
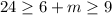
Solve the inequality
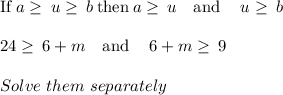

Now solve another inequality

![24\ge \:6+m\ge \:9\quad :\quad \begin{bmatrix}\mathrm{Solution:}\:&\:3\le \:m\le \:18\:\\ \:\mathrm{Interval\:Notation:}&\:\left[3,\:18\right]\end{bmatrix}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/qbxv3eu8kdkbb9cpf50idd176mdnfs0asp.png)
Thus possible values for age of Marcus is:
m = 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18