Question

Compare the wavelengths of an electron (mass = 9.11 x 10⁻³¹ kg) and a proton (mass = 1.67 x 10²⁷ kg), each having (a) a speed of 3.4 x 10⁶ m/s; (b) a kinetic energy of 2.7 x 10⁻¹⁵ J.

Answer 1

Part A:

For electron:

`\lambda_e=2.1392*10^(-10) m`

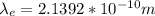
For Proton:

`\lambda_p=1.16696*10^(-13) m`

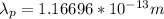
Part B:

For electron:

`\lambda_e=9.44703*10^(-12) m`

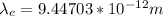
For Proton:

`\lambda_p=2.20646*10^(-13) m`

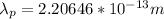
Step-by-step explanation:

Formula for wave length λ is:

`\lambda=(h)/(mv)`

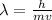
where:

h is Planck's constant=
`6.626*10^(-34)`

m is the mass

v is the velocity

Part A:

For electron:

`\lambda_e=(6,626*10^(-34))/((9.11*10^(-31))*(3.4*10^6)) \\\lambda_e=2.1392*10^(-10) m`

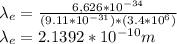
For Proton:

`\lambda_p=(6,626*10^(-34))/((1.67*10^(-27))*(3.4*10^6)) \\\lambda_p=1.16696*10^(-13) m`

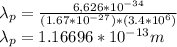
Wavelength of proton is smaller than that of electron

Part B:

Formula for K.E:

`K.E=(1)/(2)mv^2\\v=√(2 K.E/m)`

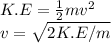
For Electron:

`v_e=\sqrt{(2*2.7*10^(-15))/(9.11*10^(-31))} \\v_e=76990597.74\ m/s`

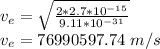
Wavelength for electron:

`\lambda_e=(6,626*10^(-34))/((9.11*10^(-31))*(76990597.74)) \\\lambda_e=9.44703*10^(-12) m`

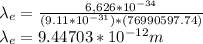
For Proton:

`v_p=\sqrt{(2*2.7*10^(-15))/(1.67*10^(-27))} \\v_p=1798202.696\ m/s`

Wavelength for proton:

`\lambda_p=(6,626*10^(-34))/((1.67*10^(-27))*(1798202.696)) \\\lambda_p=2.20646*10^(-13) m`

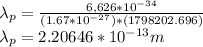
Wavelength of electron is greater than that of proton.