Answer:

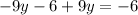
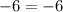
So then as we can see we can have infinite solutions.
![S= [(x, (x-2)/(3)) , x \in R]](https://img.qammunity.org/2021/formulas/mathematics/college/i3x2ofhqu8dwwwbuecq0sskw6gawou263x.png)
Explanation:
Assuming the following system of equations:
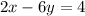 (1)
(1)
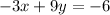 (2)
(2)
For this case we can use the substitution method in order to find the possible solutions for the system.
If we solve for x from equation (1) we got:

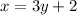 (3)
(3)
Now we can replace equation (3) into equation (2) and we got:

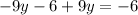
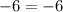
So then as we can see we can have infinite solutions.
And the possible solutions are for a fixed value of x, we can solve y from equation (3) and we got:
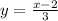
So the solution would be:
![S= [(x, (x-2)/(3)) , x \in R]](https://img.qammunity.org/2021/formulas/mathematics/college/i3x2ofhqu8dwwwbuecq0sskw6gawou263x.png)