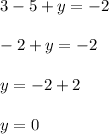Answer:

Explanation:
The complete exercise is attached.
For this exercise it is important to remember:
1. The Product of powers property. This property states that:
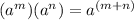
2. The multiplication of signs:
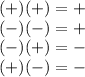
Then, given:
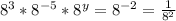
You can identify that
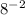 is obtained by applying the Product of powers property:
is obtained by applying the Product of powers property:

Based on the explained above, you can write the following equation:
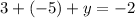
Therefore you must solve for the variable "y" in order to find its value. You get that this is: