Question

Which solution to the equation StartFraction 1 Over x minus 1 EndFraction = StartFraction x minus 2 Over 2 x squared minus 2 EndFraction is extraneous?

Answer 1

C. x = 1

Explanation:

Which solution to the equation StartFraction 1 Over x minus 1 EndFraction = StartFraction x minus 2 Over 2 x squared minus 2 EndFraction is extraneous?

x = 1 and x = –4

neither x = 1 or x = –4

x = 1

x = –4

Answer 2

Therefore x = 1 is an extraneous solution.

Explanation:

The solution to the equation StartFraction 1 Over x minus 1 EndFraction = StartFraction x minus 2 Over 2 x squared minus 2 EndFraction

`\Rightarrow (1)/(x - 1) = (x- 2)/(2x^2-2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 2x^2 - 2 = (x-1)(x-2)`

therefore
`2x^2 - 2 = x^2 - 3x + 2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x^2 + 3x - 4 = 0`

therefore
`x^2 + 3x - 4 = 0 \hspace{0.3cm} \Rightarrow = \hspace{0.3cm} (x-1)(x+4) = 0 \\`

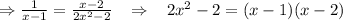
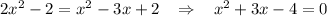
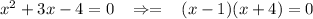
therefore x = 1 and x = -4 but we can see that if we place x = 1 in the original solution then
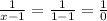`(1)/(x-1) = (1)/(1-1) = (1)/(0)` which is indeterminate.

Therefore x = 1 is an extraneous solution.