Question

PLEASE HELPPPP WITH THISSSSS

Answer 1

2) Option 9.4 is correct

Therefore the length of the given line segment is
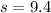`s=9.4` units

3) Option (1,1) is correct

Therefore the midpoint of the given line segment is M=(1,1)

Explanation:

2) Given that the line segment CD with endpoints C at (-3,1) and endpoint at D (5,6)

To find the length of the given line segment :

That is to find the distance of the end points using distance formula

`s=√((x_2-x_1)^2+(y_2-y_1)^2)` units

Let
`(x_1,y_1)` and
`(x_2,y_2)` be the given points (-3,1) and (5,6) respectively

Substitute the points in the distance formula we have

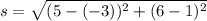`s=√((5-(-3))^2+(6-1)^2)` units

`=√((5+3)^2+(5)^2)` units

`=√(8^2+5^2)`

`=√(64+25)`

`=√(89)`

`=9.4`

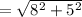
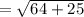
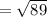
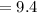
Therefore
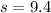`s=9.4` units

Option 9.4 is correct

Therefore the length of the given line segment is
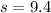`s=9.4` units

3) Given that the line segment PG with point P at (-6,4) and point at G (8,-2)

To find the midpoint of the given line segment :

Midpoint formula is
`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`

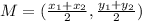
Let
`(x_1,y_1)` and
`(x_2,y_2)` be the given points (-6,4) and (8,-2) respectively

Substituting the points in the midpoint formula we get

`M=((-6+8)/(2),(4-2)/(2))`

`=((2)/(2)+(2)/(2))`

`=(1,1)`

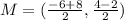
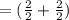
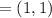
Therefore M=(1,1)

Therefore option (1,1) is correct

Therefore the midpoint of the given line segment is (1,1)