Question

A paper company needs to ship paper to a large printing business. The paper will be shipped in small boxes and large boxes. Each small box of paper weighs 45 pounds and each large box of paper weighs 80 pounds. There were twice as many large boxes shipped as small boxes shipped and the total weight of all boxes was 1435 pounds. Determine the number of small boxes shipped and the number of large boxes shipped.

Answer 1

There were 7 small boxes and 14 large boxes shipped.

Explanation:

This problem may be solved by a system of equations:

I am going to say that:

x is the number of small boxes used

y is the number of large boxes used

There were twice as many large boxes shipped as small boxes shipped

This means that
`y = 2x`

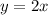
Each small box of paper weighs 45 pounds and each large box of paper weighs 80 pounds. The total weight of all boxes was 1435 pounds.

This means that
`45x + 80y = 1435`

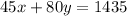
So we have to solve the following system:

`y = 2x`

`45x + 80y = 1435`

`45x + 80(2x) = 1435`

`205x = 1435`

`x = (1435)/(205)`

`x = 7`

`y = 2x = 2(7) = 14`

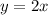
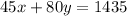
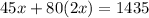
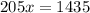
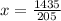
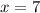
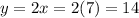
There were 7 small boxes and 14 large boxes shipped.