Answer:
a) 0.0629
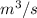 ,ρ1=31.76
,ρ1=31.76
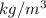 ,0.05688
,0.05688
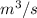
b) 0.06171
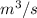 ,32.40966
,32.40966
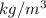 0.05498
0.05498
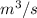
c) 0.004%
given data:
n=2 kg/s
R=188.92 J/kgK
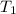 =500 K
=500 K
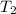 =450 K
=450 K
solution:
a) as we know ideal gas relation
PV=nRT..........(1)
The volume flow rate of inlet is
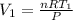 ..................(2)
..................(2)
putting the value in eq(2)
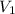 =0.0629
=0.0629
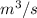
to find destiny
ρ1=
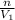 ...........................................(3)
...........................................(3)
putting value of n and V1 is eq 3
ρ1=31.76
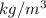
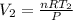 ............(A)
............(A)
putting value in eq A
=0.05688
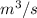
to find the rates from the compressibility factors we have to find the reduced pressure and temperature in both cases
P(reduced 1)=
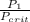 =
=
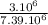 =0.41
=0.41
T(reduced 1)=
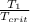 =
=
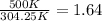
b) After looking at the chart we obtain
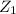 =0.98 now the volume flow rate at the inlet is:
=0.98 now the volume flow rate at the inlet is:
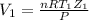 ....................................................(4)
....................................................(4)
Putting the values in eq(4)
=0.06171
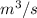
Now the density is
ρ=
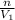
=32.40966
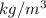
now the reduced pressure and compressibility factor in second case will be
T(reduced 2)=
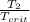 =
=
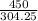 =1.48
=1.48
P(reduced 2)=P(reduced 1)=0.41
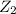 =0.97
=0.97
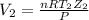 ............................................(5)
............................................(5)
putting value in eq (5)
=0.05498
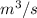
c) now find the error
Δn/n=modulus(ρ1
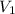 -n/n)*100%.....................(6)
-n/n)*100%.....................(6)
putting the value in eq 6
=0.004%