Answer:
(a)
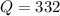
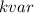 and
and
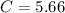
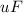
(b)
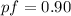 lagging
lagging
Step-by-step explanation:
Given Data:
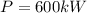
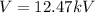
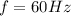
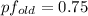
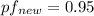
(a) Find the required kVAR rating of a capacitor
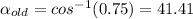 °
°
 °
°
The required compensation reactive power can be found by
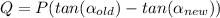
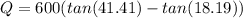
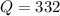
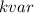
The corresponding capacitor value can be found by
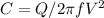
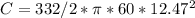
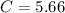
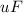
(b) calculate the resultant supply power factor
First convert the hp into kW

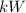
Find the electrical power (real power) of the motor
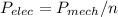
where
 is the efficiency of the motor
is the efficiency of the motor
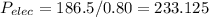
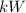
The current in the motor is

The pf of motor is 0.85 Leading
Note that
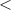 represents the angle in complex notation (polar form)
represents the angle in complex notation (polar form)
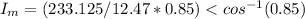
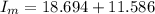
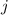

Now find the Load current
pf of load is 0.75 lagging (notice the minus sign)
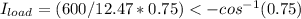
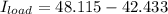

Now the supply current is the current flowing in the load plus the current flowing in the motor
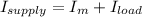
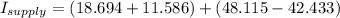
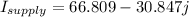

or in polar form
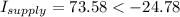 °
°
Which means that the supply current lags the supply voltage by 24.78
therefore, the supply power factor is
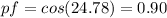 lagging
lagging
Which makes sense because original power factor was 0.75 then we installed synchronous motor which resulted in improved power factor of 0.90