Question

Please Help!!!

Answer choices listed below...

What is a polynomial function in standard form with zeroes 1, 2, -3, and -1 ?

Answer 1

Option A:

`g(x) =x^4+x^3-7x^2-x+6`

Solution:

Given data: Zeroes are 1, 2, –3, and –1.

To find the polynomial of the function for the given zeroes.

If 1 is a root of the polynomial then the factor is (x – 1).

If 2 is a root of the polynomial then the factor is (x – 2).

If –3 is a root of the polynomial then the factor is (x – (–3)) = (x + 3).

If –1 is a root of the polynomial then the factor is (x – (–1)) = (x + 1).

On multiplying the factors, we get the polynomial of the function.

`\Rightarrow\ g(x)=(x-1)(x-2)(x+3)(x+1)`

`\Rightarrow\ \ \ \ \ \ \ \ =(x^2-2x-x+2)(x^2+x+3x+3)`

`\Rightarrow\ \ \ \ \ \ \ \ =(x^2-3x+2)(x^2+4x+3)`

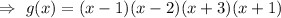
Now multiplying each term of the first factor by each term of the second.

`\Rightarrow\ \ \ \ \ \ \ \ =x^2(x^2+4x+3)-3x(x^2+4x+3)+2(x^2+4x+3)`

`\Rightarrow\ \ \ \ \ \ \ \ =(x^4+4x^3+3x^2)+(-3x^3-12x^2-9x)+(2x^2+8x+6)`

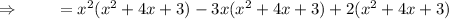
Removing brackets in each term.

`\Rightarrow\ \ \ \ \ \ \ \ =x^4+4x^3+3x^2-3x^3-12x^2-9x+2x^2+8x+6`

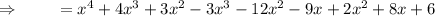
Combine the like terms and simplifying.

`\Rightarrow\ \ \ \ \ \ \ \ =x^4+4x^3-3x^3+3x^2-12x^2+2x^2-9x+8x+6`

`\Rightarrow\ \ \ \ \ \ \ \ =x^4+x^3-7x^2-x+6`

`\Rightarrow \ g(x) =x^4+x^3-7x^2-x+6`

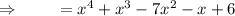
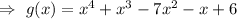
Option A is the correct answer.

Hence
`g(x) =x^4+x^3-7x^2-x+6`.