Question:
The image of the question is attached below.
Answer:
x = 40
Solution:
Given ΔVDG
 ΔVNG.
ΔVNG.
DG = 207, NQ = 138, GQ = 60, QV = x
In two triangles are similar, then the measures of the corresponding sides are in proportional to each other.
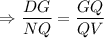
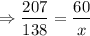
Do cross multiplication, we get
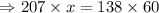
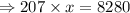
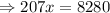
Divide by 207 on both sides of the equation, we get
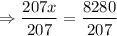

⇒ x = 40
⇒ QV = 40
Hence the value of x is 40.