Question

Triangle VDG- triangle VNQ
What is the value of x?
Enter your answer in the box.

Answer 1

its 8

Explanation:

Answer 2

Question:

The image of the question is attached below.

Answer:

x = 40

Solution:

Given ΔVDG
`\sim` ΔVNG.

DG = 207, NQ = 138, GQ = 60, QV = x

In two triangles are similar, then the measures of the corresponding sides are in proportional to each other.

`$\Rightarrow(DG)/(NQ)=(GQ)/(QV)`

`$ \Rightarrow(207)/(138)=(60)/(x)`

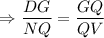
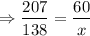
Do cross multiplication, we get

`$ \Rightarrow{207* x}=138*60`

`$ \Rightarrow{207* x}=8280`

`$ \Rightarrow{207x}=8280`

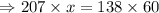
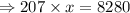
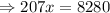
Divide by 207 on both sides of the equation, we get

`$ \Rightarrow\frac{{207x}}{207} =(8280)/(207)`

`$ \Rightarrow x =(8280)/(207)`

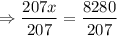
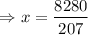
⇒ x = 40

⇒ QV = 40

Hence the value of x is 40.