Element X decays radioactively with a half-life of eight minutes. If there are 800 g of element X, how long, to the nearest 10th of a minute, would it take the element to decay …

Question

asked Sep 2, 2021 84.3k views

1 Answer

Geanette · Answer 1 · 2021-09-07T04:58:58+0000

Answer: 41.5 min

Explanation:

This problem can be solved with the Radioactive Half Life Formula:

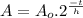$A=A_(o).2^{(-t)/(h)}$ (1)

Where:

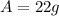A=22 g is the final amount of the radioactive element

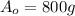A_(o)=800 g is the initial amount of the radioactive element

is the time elapsed

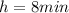h=8 min is the half life of the radioactive element

So, we need to substitute the given values and find
from (1):

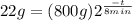$22 g=(800 g) 2^{(-t)/(8 min)}$ (2)

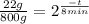$(22 g)/(800 g)=2^{(-t)/(8 min)}$ (3)

$(11)/(400)=2^{(-t)/(8 min)}$ (4)

Applying natural logarithm in both sides:

$ln((11)/(400))=ln(2^{(-t)/(8 min)})$ (5)

-3.593=-(t)/(8 min)ln(2) (6)

Clearing
:

$t=41.46 min \approx 41.5 min$ This is the time elapsed