Answer:
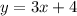is parallel to
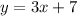
Explanation:
The complete exercise is: "Is
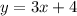parallel, perpendicular or neither to
?"
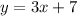The equation of the line in Slope-Intercept form is:
Where "m" is the slope of the line and "b" is the y-intercept.
First, in order to solve this exercise it is important to remember that, by definition:
1. The slopes of parallel lines are equal.
2. The slopes of perpendicular lines are negative reciprocal.
In this case, you have the following line given in the exercise:
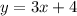
You can identify that "m" and "b" are:
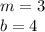
And the other line provided in the exercise is this one:
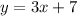
So, you can identify that:
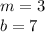
As you can notice, the slopes of both lines are equal; therefore, you can conclude that those lines are parallel.