Question

A parabola with the equation y=-2x+4x+3 is intercepted by a line with the slope of 1 that passes through the y-intercept of the parabola. Which is the other point of intersection.

Answer 1

The other point of intersection is (1.5,4.5)

Explanation:

The correct quadratic equation is

`y=-2x^2+4x+3`

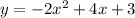
step 1

Find he y-intercept of the parabola

The y-intercept is the value of y when the value of x is equal to zero

so

For x=0

`y=-2(0)^2+4(0)+3=3`

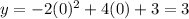
therefore

The y-intercept is the point (0,3)

step 2

Find the equation of the line

The equation in slope intercept form is

`y=mx+b`

we have

`m=1\\b=3`

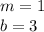
substitute

`y=x+3`

step 3

Find the other point of intersection

we have

`y=-2x^2+4x+3`

`y=x+3`

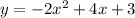
Equate both equations

`-2x^2+4x+3=x+3`

solve for x

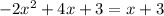
`-2x^2+3x=0`

`2x^2=3x`

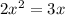
we know that one solution is x=0

simplify x

`2x=3\\x=1.5`

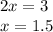
Find the value of y

substitute the value of x in any equation (line or parabola)

`y=1.5+3=4.5`

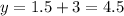
therefore

The other point of intersection is (1.5,4.5)