Question

PLEASE HELP QUICKLY!!

Which integral gives the area of the region in the first quadrant bounded by the x-axis, y = x2, and x + y = 2?

the integral from 0 to 2 of x squared minus the quantity 2 minus x, dx

the integral from 0 to 1 of x squared, dx plus the integral from 1 to 2 of the quantity 2 minus x, dx

the integral from 0 to 1 of x squared, dx minus the integral from 1 to 2 of the quantity 2 minus x, dx

the integral from 0 to 2 of the difference of 2 minus x and x squared, dx

Answer 1

Answer:
`\displaystyle \int_(0)^(1)x^2dx + \int_(1)^(2)(2-x)dx`

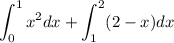
Which is choice B

==========================================

Step-by-step explanation:

See the diagram below.

x+y = 2 is the same as y = 2-x

f(x) = x^2 and g(x) = 2-x intersect at (1,1) which is where we split the integrals so we have two regions to worry about

------------------

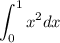`\displaystyle \int_(0)^(1)x^2dx` shown in red in the diagram represents the area under y = x^2 from x = 0 to x = 1

-------------------

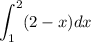`\displaystyle \int_(1)^(2)(2-x)dx`shown in blue (same diagram) represents the area under y = 2-x from x = 1 to x = 2.

-------------------

Combining the two integrals gets us the total area bounded by

• the x axis
• y = x^2
• x+y = 2