Answer:
it makes more sense to buy one 20 inch pizza
Explanation:
step 1
Find the area of a 10 inch pizza
The area of a pizza ( circle) is equal to
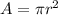
we have
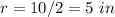 ---> the radius is half the diameter
---> the radius is half the diameter
substitute
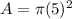
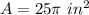
assume
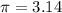
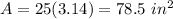
step 2
Find the cost of a 10 in pizza per square inch
Divide the cost by the area
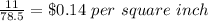
step 3
Find the area of a 20 inch pizza
The area of a pizza ( circle) is equal to
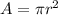
we have
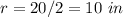 ---> the radius is half the diameter
---> the radius is half the diameter
substitute
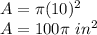
assume
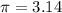
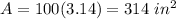
step 4
Find the cost of a 20 in pizza per square inch
Divide the cost by the area
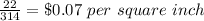
therefore
it makes more sense to buy one 20 inch pizza (because the unit rate is less)