Question

A rock is thrown upward with a velocity of 24 meters per second from the top of a 20 meter high cliff, and it misses the cliff on the way back down. When will the rock be 7 meters from ground level? Round your answer to two decimal places.

Answer 1

The rock will be 7 meters from ground level after 0.62 s and 4.28 s

When will the rock be 7 meters from ground level?

From the question, we have the following parameters that can be used in our computation:

Velocity = 24 m/s

Initial height = 20 m

The function of the height can be expressed as

f(t) = -1/2gt² + vt + h

Where

g = 9.8m/s² --- gravity acceleration

v = 24m/s --- initial velocity

h = 20 --- initial height

Substitute the known values into the equation

f(t) = -1/2 * 9.8t² + 24t + 20

f(t) = -4.9t² + 24t + 20

At a height of 7 meters, we have

-4.9t² + 24t + 20 = 7

-4.9t² + 24t + 13 = 0

Using the quadratic formula, we have

`t = (-b \pm √(b^2 - 4ac))/(2a)`

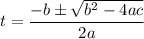
Where

a = -4.9, b = 24 and c = 13

So, we have

`t = (-24 \pm √((24)^2 - 4 * 4.9 * 13))/(2 * -4.9)`

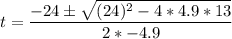
This gives

`t = (-24 \pm √(321.2))/(-9.8)`

`t = (-24 \pm 17.9)/(-9.8)`

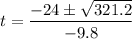
Expand

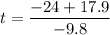`t = (-24 + 17.9)/(-9.8)\\` and
`t = (-24 - 17.9)/(-9.8)`

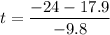
Evaluate

t = 0.62 and t = 4.28

Hence, the rock will be 7 meters from ground level after 0.62 s and 4.28 s

Answer 2

Answer: 1.19 s

Explanation:

This situation is related to parabolic motion; hence we can use the following equation to find the time the rock is 7 meters from ground level:

`y=y_(o)+V_(o)sin \theta t-(g)/(2)t^(2)` (1)

Where:

`y=20m-7m=13 m` is the height (position) of the rock when it is 7 meters from ground level (taking into account the initial position is 20 m)

`y_(o)=20 m` is the initial height of the rock

`V_(o)=24 m/s` is the rock's initial speed

`\theta=0\°` is the angle at which the rock was thrown (upward or vertically)

`t` is the time at whch the rock is in position
`y`

`g=9.8m/s^(2)` is the acceleration due gravity

Isolating
`t` from (1):

`t=\sqrt{-(2(y-y_(o)))/(g)}` (2)

Solving with the given data:

`t=\sqrt{-(2(13 m-20 m))/(9.8m/s^(2))}` (3)

`t=1.19 s` (4) This is the time at which the rock is 7 meters from ground level.