The rock will be 7 meters from ground level after 0.62 s and 4.28 s
When will the rock be 7 meters from ground level?
From the question, we have the following parameters that can be used in our computation:
Velocity = 24 m/s
Initial height = 20 m
The function of the height can be expressed as
f(t) = -1/2gt² + vt + h
Where
g = 9.8m/s² --- gravity acceleration
v = 24m/s --- initial velocity
h = 20 --- initial height
Substitute the known values into the equation
f(t) = -1/2 * 9.8t² + 24t + 20
f(t) = -4.9t² + 24t + 20
At a height of 7 meters, we have
-4.9t² + 24t + 20 = 7
-4.9t² + 24t + 13 = 0
Using the quadratic formula, we have
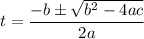
Where
a = -4.9, b = 24 and c = 13
So, we have
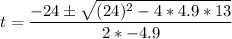
This gives
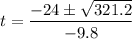

Expand
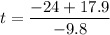 and
and
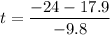
Evaluate
t = 0.62 and t = 4.28
Hence, the rock will be 7 meters from ground level after 0.62 s and 4.28 s