Question

A new car striaght line depreciates according to the equation y=-1,875x + 20,625. What is the original price of the car? How many years will it take for this car to fully striaght line depreciate?

Answer 1

The original price of the car = $20,625

It will take 11 years or this car to fully straight line depreciate.

Explanation:

Given:

The straight line depreciation of a car is given as:

`y=-1,875x+20,625`

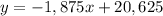
To find the original price of the car and the number of years it takes for this car to fully straight line depreciate.

Solution:

The straight line depreciation equation is given as:

`y=-mx+b`

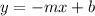
where
`m` represents the rate of depreciation per year,
`x` represents number of years and
`b` represents the original value.

From the given equation we can see that the original value
`b` is = 20,625

Thus, the original price of the car = $20,625

To find he number of years it takes for this car to fully straight line depreciate, we will substitute
`y=0` as the value of car is fully depreciated.

So, we have:

`0=-1,875x+20,625`

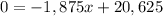
We can now solve for
`x` to get the number of years it takes for this car to fully straight line depreciate.

Adding
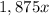`1,875x` both sides.

`0+1,875x=-1.875x+1,875x+20,625`

`1,875x=20,625`

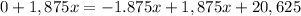
Dividing both sides by 1,875

`(1,875x)/(1,875)=(20,625)/(1,875)`

∴
`x=11`

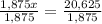
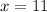
Thus, it will take 11 years or this car to fully straight line depreciate.