Answer:
Therefore,
93.6 feet tall is the tower from the ground.
Explanation:
Given:
x = Opposite side to angle 60
50 ft = Adjacent side to angle 60
7 ft = height of boy
So Height of the tower will be,
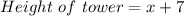
To Find:
Height of the tower = ?
Solution:
In Right Angle Triangle , Tangent Identity we have,
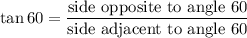
Substituting the values we get
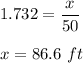
Substituting "x" For Height of tower we get

Therefore,
93.6 feet tall is the tower from the ground.