Question

What is the range of the function y=1 +2sin(x - 11 )?

OA -1 to 1
OB. 2 to 2
OC. 0 to 3
D. -1 to 3
E. =3 to 3

Answer 1

D. -1 to 3

Explanation:

We have been given a function
`y=1+2sin(x-11 )`. We are asked to find the range of the function.

We know that since oscillates between
`-1` and 1, that is minimum value of sin is
`-1` and maximum is 1.

The range of basic sin function is
`-1\leq \text{sin}(x-11)\leq 1`.

Now we will multiply all sides by 2.

`-1\cdot 2\leq 2\cdot \text{sin}(x-11)\leq 1\cdot 2`

`-2\leq 2\text{sin}(x-11)\leq 2`

Now we will add 1 on all sides as:

`-2+1\leq 2\text{sin}(x-11)+1\leq 2+1`

`-1\leq 2\text{sin}(x-11)+1\leq 3`

`-1\leq f(x) \leq 3`

Therefore, the range of the given function is
`[-1,3]` and option D is the correct choice.

Answer 2

range of the given function in Interval notation is [-1, 3]

Explanation:

i) given function is y = 1 + 2sin(x - 11)

ii) maximum of sin function is 1

iii) therefore maximum of given function
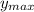`y_(max)` = 1 + (2
`*` 1) = 3

iv) minimum of sin function is -1

v) therefore maximum of given function
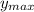`y_(max)` = 1 + (2
`*` -1) = -1

vi) therefore the range of the given function in Interval notation is [-1,3]