8 lilies and 12 tulips are in bouquet
Solution:
Let "x" be the number of lilies
Let "y" be the number of tulips
Cost of 1 lily = $ 3
Cost of 1 tulip = $ 2
A bouquet of lilies and tulips has 20 flowers
Therefore,
number of lilies + number of tulips = 20
x + y = 20
y = 20 - x ---------- eqn 1
The bouquet costs $48. Therefore, we frame a equation as:
number of lilies x Cost of 1 lily + number of tulips x number of tulips = 48
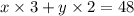
3x + 2y = 48 -------- eqn 2
Let us solve eqn 1 and eqn 2
Substitute eqn 1 in eqn 2
3x + 2(20 - x) = 48
3x + 40 - 2x = 48
x = 8
Substitute x = 8 in eqn 1
y = 20 - 8
y = 12
Thus 8 lilies and 12 tulips are in bouquet