Answer:
A rectangular lot is 100 meters wide and 150 meters long.Give the length and width of another rectangular lot that has the same perimeter but a smaller area.
The rectangular lot is having length of 170 meters and width of 80 meters.
Explanation:
Given:
A rectangle.
Length of the rectangle = 150 meters
Width of the rectangle =100 meters
So perimeter of this rectangle = 2 (width+ length)
And area of this rectangle =(width)(length)
- Perimeter =
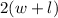
=
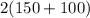
=
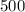 meters.
meters.
- Area =
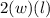
=
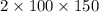
=
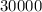 square meters.
square meters.
Now we have to find an another rectangular lot which has the same perimeter but different area.
Note: Subtract 20 m from the width and add 20m length into the longer side. (We can try with another multiple of 10).
So,
The new width = 100-20 = 80 meters.
And the new length =150+20 = 170 meters.
Lets check the perimeter and its area.
The perimeter must be equivalent to 500 meters and its area be less than 30000 sq-meters.
- Perimeter =
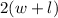
=
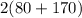
=
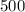 meters.
meters.
- Area =
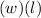
=
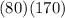
=
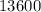 square meters.
square meters.
Hence the rectangular lot with length 170 m and with 80 m proves to have same perimeter and smaller area.