Question

A rectangular lot is 100 meters wide and 150 meters long.

Give the length and width of another rectangular lot that has the same periMeter but smaller area
width = meters
x
s
?
length = 1 meters

Answer 1

A rectangular lot is 100 meters wide and 150 meters long.Give the length and width of another rectangular lot that has the same perimeter but a smaller area.

The rectangular lot is having length of 170 meters and width of 80 meters.

Explanation:

Given:

A rectangle.

Length of the rectangle = 150 meters

Width of the rectangle =100 meters

So perimeter of this rectangle = 2 (width+ length)

And area of this rectangle =(width)(length)

• Perimeter =
  `2(w+l)`

=
`2(150+100)`

=
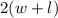
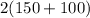
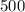`500` meters.

• Area =
  `2(w)(l)`

=
`2* 100* 150`

=
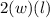
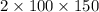
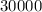`30000` square meters.

Now we have to find an another rectangular lot which has the same perimeter but different area.

Note: Subtract 20 m from the width and add 20m length into the longer side. (We can try with another multiple of 10).

So,

The new width = 100-20 = 80 meters.

And the new length =150+20 = 170 meters.

Lets check the perimeter and its area.

The perimeter must be equivalent to 500 meters and its area be less than 30000 sq-meters.

• Perimeter =
  `2(w+l)`

=
`2(80+170)`

=
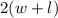
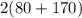
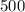`500` meters.

• Area =
  `(w)(l)`

=
`(80)(170)`

=
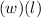
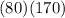
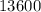`13600` square meters.

Hence the rectangular lot with length 170 m and with 80 m proves to have same perimeter and smaller area.