Answer:
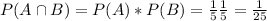
So then the best option would be:
a. 1/25
Explanation:
For this case we assume that the sample space for the numbers is :
![S_1= [A,B,C,D,E]](https://img.qammunity.org/2021/formulas/mathematics/college/ekbvhfonvyrou73x5ibw2sya7hynmsrz62.png)
And the sample space for the numbers is:
![S_2 =[1,2,3,4,5]](https://img.qammunity.org/2021/formulas/mathematics/college/3s8t3v5q4l9vdpg3f8xty5qd7o08uja6c3.png)
Both sampling spaces with a size of 5.
We define the following events:
A="We select a 2 from the numbers"
B= "We select a E from the letters"
We can find the individual probabilities for each event like this:
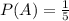
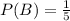
And assuming independence we can find the probability required like this:
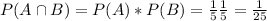
The last probability is the probability of obtain obtain a 2 AND an E
So then the best option would be:
a. 1/25