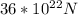To solve this problem we will use the related concepts in Newtonian laws that describe the force of gravitational attraction. We will use the given value and then we will obtain the proportion of the new force depending on the Radius. From there we will observe how much the force of attraction increases in the new distance.
Planet gravitational force
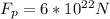
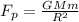
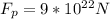
Distance between planet and star
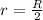
Gravitational force is
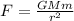
Applying the new distance,
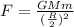
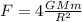
Replacing with the previous force,
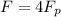
Replacing our values
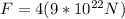
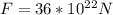
Therefore the magnitude of the force on the star due to the planet is