Answer:
Distance between ice-cream parlor and candy store is 4.6 miles.
Explanation:
We have drawn the diagram for your reference.
Given:
ice cream parlor that is due south of his school at 2 miles.
So According to diagram:
SI = 2 miles
Also Given:
school and the straight-line distance between the school and the candy is 5 miles which is in west.
SC = 5 miles
We need to find the distance between ice-cream parlor and candy store.
According to diagram We need to find IC.
Solution:
Let us assume Δ ISC to be right angled triangle.
Then we will apply Pythagoras theorem we get;
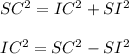
Substituting the values we get;
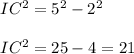
Now taking square root on both side we get;
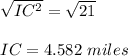
Rounding to nearest tenth we get;
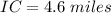
Hence distance between ice-cream parlor and candy store is 4.6 miles.