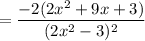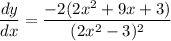Option A:
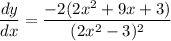
Solution:
Given
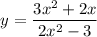
To calculate
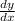 :
:
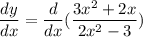
Using differential rule:
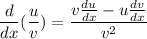
Here,
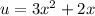 and
and
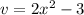
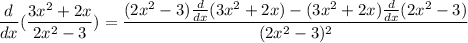 – – – – (1)
– – – – (1)
Now, using another differential rule:
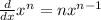 and
and
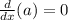 , a=constant
, a=constant
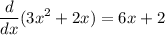 – – – – (2)
– – – – (2)
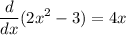 – – – – (3)
– – – – (3)
Substitute (2) and (3) in (1), we get
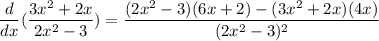
Now, simplifying the above equation
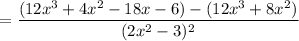
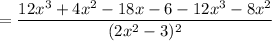
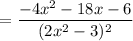
Take –2 as common factor in numerator of the fraction.