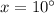Question

This is all of Geometry work

Answer 1

9. x = 9 units

10.
`x^\circ = 12^\circ`

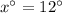
11.
`x^\circ = 6^\circ`

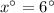
12.x =10 units

13. x= 1 unit

14.
`x =3^\circ`

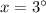
15.
`x = 10^\circ`

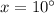
16.
`x = 10^\circ`

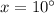
Explanation:

9.

Opposite sides of a parallelogram are equal to each other.

Therefore

2x-5 = 13

⇔2x = 13+5

⇔
`x = (18)/(2)`

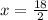
⇔x = 9 units

10.

Sum of adjacent angles of parallelogram is
`180^\circ`.

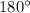Therefore

`(11x-7)^\circ +55= 180 ^\circ`

⇔
`11x^\circ = 180 ^\circ -55^\circ +7^\circ`

⇔
`11x^\circ = 132^\circ`

⇔
`x^\circ=((132)/(11) )^\circ`

⇔
`x^\circ = 12^\circ`

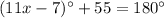
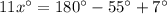
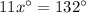
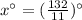
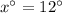
11.

Opposite angles of a parallelogram are congruent(equal).

Therefore

`16x -4 = 92^\circ`

⇔
`16x = 92^\circ +4`

⇔
`x^\circ =(96 )/(16)`

⇔
`x^\circ = 6^\circ`

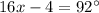
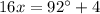
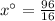
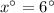
12.

Opposite sides of a parallelogram are congruent.

Therefore

2x-11=9

⇔2x = 11+9

⇔2x=20

⇔
`x =(20)/(2)`

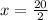
⇔x =10 units

13.

Opposite sides of a parallelogram are congruent (equal).

Therefore,

17x+1=18

⇔17x =18-1

⇔x= 1 unit

14.

Opposite angles of a parallelogram are congruent(equal).

Therefore,

`12x -1 =35^\circ`

⇔
`12x =35^\circ +1^\circ`

⇔
`x= ((36)/(12) )^\circ`

⇔
`x =3^\circ`

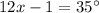
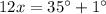
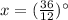
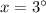
15.

Sum of adjacent angles of parallelogram is
`180^\circ`.

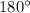Therefore

`10x +6 + 74^\circ=180^\circ`

⇔
`10x =180^\circ -74^\circ -6^\circ`

⇔
`x =( (100)/(10) )^\circ`

⇔
`x = 10^\circ`

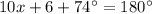
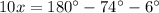
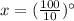
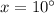
16.

Opposite angles of a parallelogram are congruent(equal).

Therefore,

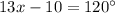
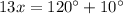
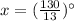
`13x -10=120^\circ`

⇔
`13x = 120^\circ +10^\circ`

⇔
`x =( (130)/(13))^\circ`

⇔
`x = 10^\circ`