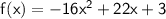
Part A
To find x-intercepts, the f(x) will be 0

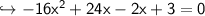
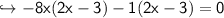
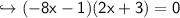
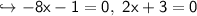
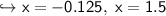
find y-intercept:
to find y-intercept, x will be 0
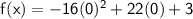

Part B
To find vertex use the formula: x = -b/2(a)
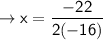
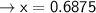
find y coordinates:
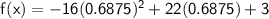
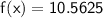
coordinates of vertex: (0.6875, 10.5625)
As its positive and greater than 0, the vertex will be Maximum.
part C
To draw the graph, simplify point the vertex on the graph. Then point both the x-intercepts. Also the y-intercept and draw the curve with free hand.
Graph attached: