Question

In a state where license plates contain six digits, what is the probability that the license number of a randomly selected car has exactly two 9's? Assume that each digit of the license number is randomly selected from .

Answer 1

Explanation:

Given : In a state where license plates contain six digits.

Probability of that a number is 9 =
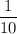`(1)/(10)` [Since total digits = 10]

We assume that each digit of the license number is randomly selected .

Since each digit in the license plate is independent from the other and there is only two possible outcomes for given case (either 9 or not), so we can use Binomial.

Binomial probability formula:
`P(X=x)=^nC_xp^x(1-p)^(n-x)`

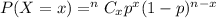
, where n= total trials , p = probability for each success.

Let x be the number of 9s in the license plate number.

`X\sim Bin(n=6, p=(1)/(10)})`

Then, the probability that the license number of a randomly selected car has exactly two 9's will be :

`P(X=2)=^6C_2((1)/(10))^2(1-(1)/(10))^(6-2)\\\\=(6!)/(2!(6-2)!)((1)/(100))((9)/(10))^4=0.098415`

Hence, the required probability = 0.098415