Answer:
The experimental molar absorptivity constant for the nickel(II) sulfate solution is
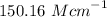 .
.
Step-by-step explanation:
According to the Lambert's Beer law:-
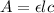
Where, A is the absorbance
l is the path length
is the molar absorptivity
c is the concentration.
Given that:-
The nickel(II) sulfate is 0.07973 % w/v in concentration
It means that 0.07973 g of nickel(II) sulfate is present in 100 mL of solution.
Molar mass of
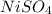 = 154.75 g/mol
= 154.75 g/mol
The formula for the calculation of moles is shown below:
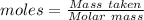
Thus,
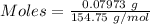
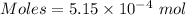
Volume = 100 mL = 0.1 L (1 mL = 0.001 L )
Thus, Molarity can be calculated as:-
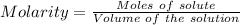
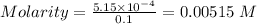
Path length = 1.20 cm
A = 0.928
So, applying the values in the Lambert Beer's law as shown below:-
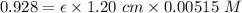
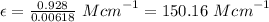
The experimental molar absorptivity constant for the nickel(II) sulfate solution is
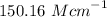 .
.