Question

A student prepared a solution containing 0.07973% (w/v) of nickel(II) sulfate and measured its absorbance, The experimental absorbance was 0.928. Calculate the experimental molar absorptivity constant for the nickel(II) sulfate solution if the path of length of light was determined to be 1.20cm. Show ALL your work. Your final value should have the correct unit and number of significant figures. Molecular weight for N_iSO_4 = 154.75%g/mol. Refer to w/v examples shown on bottom of this page.

Answer 1

The experimental molar absorptivity constant for the nickel(II) sulfate solution is
`150.16\ {M cm}^(-1)`.

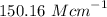Step-by-step explanation:

According to the Lambert's Beer law:-

`A=\epsilon l c`

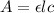
Where, A is the absorbance

l is the path length

is the molar absorptivity

c is the concentration.

Given that:-

The nickel(II) sulfate is 0.07973 % w/v in concentration

It means that 0.07973 g of nickel(II) sulfate is present in 100 mL of solution.

Molar mass of
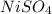`NiSO_4` = 154.75 g/mol

The formula for the calculation of moles is shown below:

`moles = (Mass\ taken)/(Molar\ mass)`

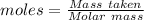
Thus,

`Moles= (0.07973\ g)/(154.75\ g/mol)`

`Moles= 5.15* 10^(-4)\ mol`

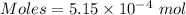
Volume = 100 mL = 0.1 L (1 mL = 0.001 L )

Thus, Molarity can be calculated as:-

`Molarity=(Moles\ of\ solute)/(Volume\ of\ the\ solution)`

`Molarity=(5.15* 10^(-4))/(0.1)=0.00515\ M`

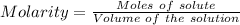
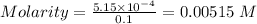
Path length = 1.20 cm

A = 0.928

So, applying the values in the Lambert Beer's law as shown below:-

`0.928=\epsilon* 1.20\ cm* 0.00515\ M`

`\epsilon=(0.928)/(0.00618)\ {M cm}^(-1)=150.16\ {M cm}^(-1)`

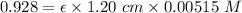
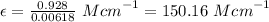
The experimental molar absorptivity constant for the nickel(II) sulfate solution is
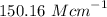`150.16\ {M cm}^(-1)`.