Answer:
q = 0.75 nC
Step-by-step explanation:
We know that the downward gravitational force is balanced by the upward static friction force.
This static friction force is one of the components of the contact force (the other being the normal force, perpendicular to the friction force), and can be expressed as a fraction of the normal force, as follows:
Ff = μ*N
⇒ μ*N = m*g (1)
In the other way, we know that this normal force is supplied by the electrostatic force between the charges in the charged balloon and the ones induced in the wall molecules.
Assuming that we can treat these charges as point charges separated by 0.5 mm, they must obey the Coulomb's Law, as follows:
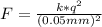 (2)
(2)
From (1) we can solve for N, as follows:
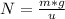 (3)
(3)
As (2) and (3) are equal each other (as they are different ways to express the normal force, and the only unknown that we have is q, we can solve this equality for q, as follows:
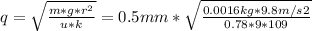
⇒ q = 0.75 nC