Answer: 0.336
Explanation:
Let x be the number of students who take the SAT each year receive special accommodations.
Probability that a student who take the SAT each year receive special accommodations =0.03
Here ,
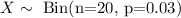
Binomial probability formula :
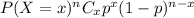 , where p =probability of each successes , n is total trials.
, where p =probability of each successes , n is total trials.
Then ,
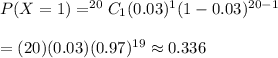
Hence, the probability that exactly 1 received a special accommodation is 0.336 .