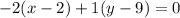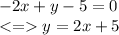Question

Find the equation (in terms of x) of the line through the points (-2,1) and(2,9)
Y=

Answer 1

y = 2x + 5

Explanation:

There are 2 ways to find this equation:

The first way: We have: y = ax + b (this is the line, right?)

The line is through the point (-2, 1) so we have:

1 = (-2)a + b (1)

The line is also through the point (2, 9) so we have:

9 = 2a + b. (2)

From (1) and (2) we get a equals 2, b equals 5. Then:
y = 2x + 5

The second way:

Let A(-2, 1) and B(2, 9), then AB = (4, 8).

=> The normal vector of this line is n = (-2, 1).

The line that is through the points A(-2, 1) and B(2, 9), and has the normal vector n=(-2, 1) has the equation:

`-2(x - 2) + 1(y - 9) = 0`

`-2x + y - 5 =0\\ < = > y = 2x + 5`

Answer 2

2

Explanation:

gradient =y² -y¹ /x²-x¹

=9-1/2--2

=8/4

=2