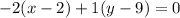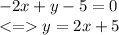Answer:
y = 2x + 5
Explanation:
There are 2 ways to find this equation:
The first way: We have: y = ax + b (this is the line, right?)
The line is through the point (-2, 1) so we have:
1 = (-2)a + b (1)
The line is also through the point (2, 9) so we have:
9 = 2a + b. (2)
From (1) and (2) we get a equals 2, b equals 5. Then:
y = 2x + 5
The second way:
Let A(-2, 1) and B(2, 9), then AB = (4, 8).
=> The normal vector of this line is n = (-2, 1).
The line that is through the points A(-2, 1) and B(2, 9), and has the normal vector n=(-2, 1) has the equation: